Q:
给你一个整数 n ,按字典序返回范围 [1, n] 内所有整数。
你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。
S:
首先:字典序可以抽象为一棵树,如下图所示
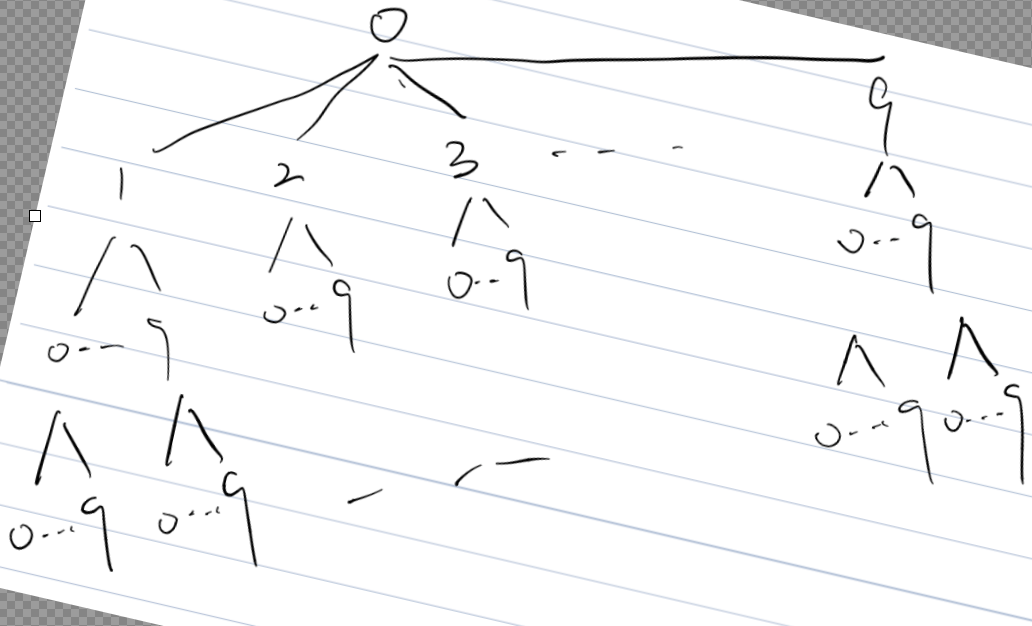
所以,有小到大输出其实就是输出他的先序遍历
参考二叉搜索树的先序遍历写法
1.递归:
此处不一样的是需要舍去头结点0,以1-9分别为根节点进行遍历输出:
1.递归结束条件,当前结点>n,则递归结束
2.将元素值添加进入res,遍历其10个兄弟结点,进入递归其子节点
1 | ```java |
2.迭代:
tipp :while(curr%10==0) curr/=10; 这行代码的目的是处理那些在字典序中应该提前结束的数字。
例如,假设 n 是 130。我们在字典序中遍历时,应该是这样的顺序:1, 10, 11, …, 19, 2, 20, …, 29, …, 13, 130, 14, …, 19, 2, …, 9。
当我们的 curr 变成 130 后,如果我们直接 curr+=1,那么 curr 就变成了 131,这显然是超过 n 的,而且不符合字典序。我们应该跳过所有 13x(x > 0)的数字,直接变成 14。
这就是 while(curr%10==0) curr/=10; 这行代码的目的:当 curr 的最后一位是 0(即 curr%10==0)时,我们应该退回到上一层(即 curr/=10)。在这个例子中,130 退回到 13,然后 curr+=1 变成 14,这样就符合字典序了。
这样的处理能保证我们的遍历顺序始终是按照字典序进行的,即先遍历同一层的数,然后再遍历下一层的数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public List<Integer> lexicalOrder(int n) {
List<Integer> list = new ArrayList<>();
int curr = 1;
// 遍历/traverse
for(int i=0;i<n;i++){
list.add(curr);
if(curr*10<=n){
curr*=10;//遍历下一层/find next level number
}else{
if(curr>=n) curr/=10;//如果比n大,结束遍历退回上一层/If greater than n, end traversal and return to previous level
curr+=1;
while(curr%10==0) curr/=10;
}
}
return list;
}
}