Binary Indexed Tree with applications in LeetCode
Why need Binary Indexed Tree
QA:
Suppose there exists a sequence of integers input, e.g.
intput = [1,2,7,4,3], requiring the sum of the first K numbers.Sulotion:
Generally we will find a prefix and array
preSumArray, wherepreSumArray[i]represents the sum of the firstinumbers, so that we find the sum of the first N numbers only need to returnpreSumArray[N], the time complexity is O(1), if you need to query K times, the complexity is O(K).QA:
Suppose there exists a sequence of integers input, e.g.
intput = [1,2,7,4,3], now when we get the sum of the first N numbers, we might first increase/decrease the number at positionibyvalue.Sulotion:
Generally we will find a prefix sum array
preSumArray, wherepreSumArray[i]represents the sum of the firstinumbers, as shown in the previous problem, we can still get the prefix sum in O(1) time. But if we need to insert a numberxat positioni, we need to update allpreSumArrayafteriwhen we do the update, at which point the single update time is O(N) and the complexity of the K queries is O(KN). If we do not usepreSumArray, then the update complexity is O(1), and the query complexity becomes O(N).This is where Binary Indexed Tree can help us solve this problem quickly.
There are many interesting applications of binary which could probably be summarised somewhat subsequently, but here is a usage of
lowbit(x) = x&(-x)The purpose of this equation is to find the largest power of 2 that can divide X, which is the rightmost 1 of X. This purpose is important.
For example:
5&-5 = 1;10&-10 = 2;12&-12 = 4Principle:
Generally integers are stored in computers using a complement code, where a negative number is equivalent to taking each bit and inverting it, and then adding 1 to the low bit.
For example
10 = 1010,-10 = 0110, solowbit(10) = 2Binary Indexed Tree,BIT
Essentially it is still an array, and is similar to
preSumArrayin that it still holds the sum array, but it holds the sum of i bits up to and including i, and lowbit(i) integers. This can be represented by the following diagram and the formula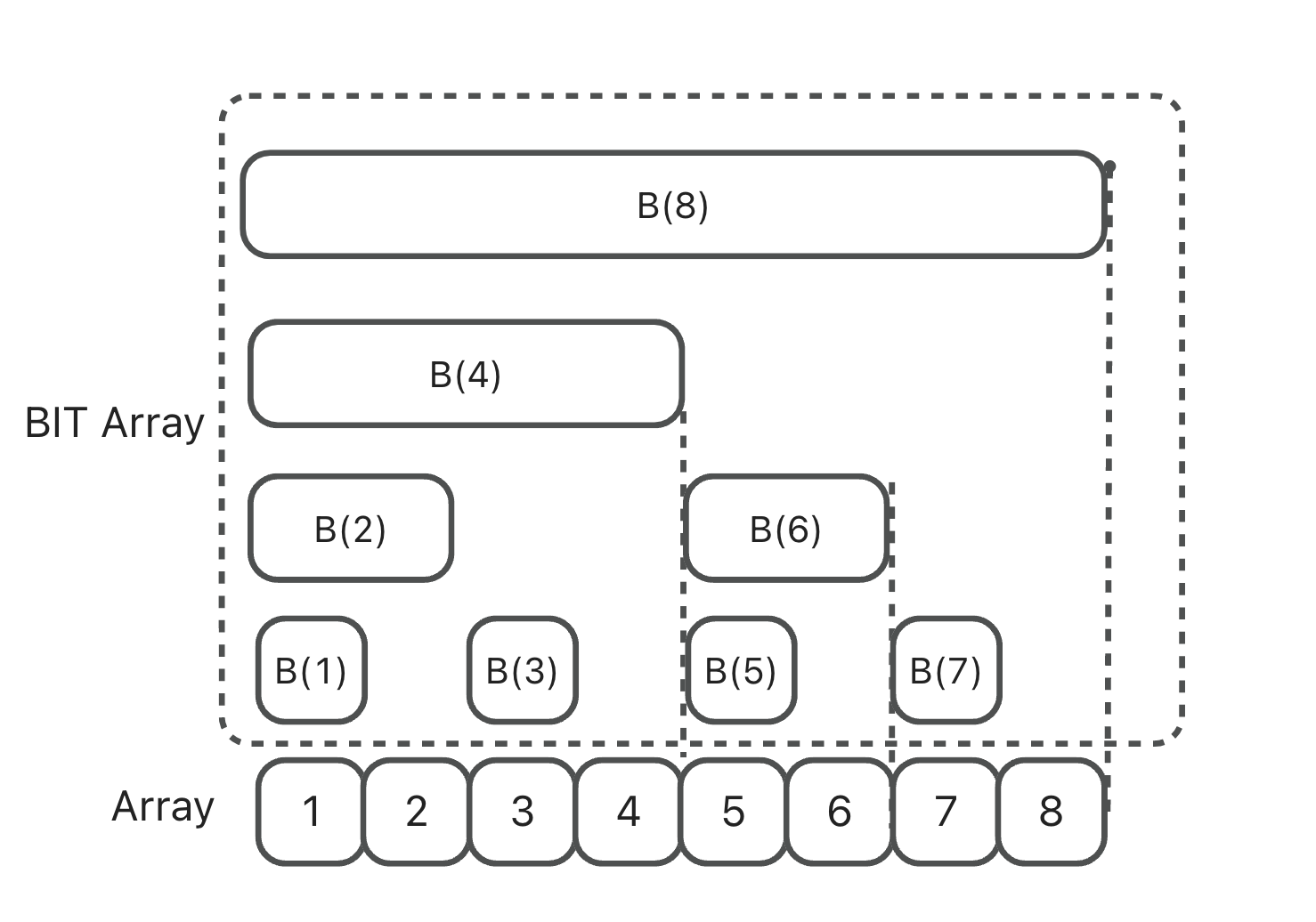
1
2
3
4
5
6
7
8
9B(1) = A(1);
B(2) = A(1)+A(2);
B(3) = A(3);
B(4) = A(1)+A(2)+A(3)+A(4);
B(5) = A(5);
B(6) = A(5)+A(6);
B(7) = A(7);
B(8) = A(1)+A(2)+A(3)+A(4)+A(5)+A(6)+A(7)+A(8);tip: BIT index must start with 1.
Achieving
Now based on BIT, we need to solve the 2 previous problems - summation and update.
getSum
Suppose we have a function getSum(i), which finds the sum of all numbers from 1 to i. The next step is to implement it. The next step is how to implement it.
As an example.
getSum(7) = A(1) +... +A(7) = B(4)+B(6)+B(7)getSum(6) = B(4)+B(6)Now the question is, how do you put
A(1)+.... +A(i)to the stump array corresponding to those items:First: B(i) is defined as the sum of the first lowbit(i) starting from A(i), so we can get
$$
B(i) = A(i-lowbit(i)+1)+… +A(i)\
$$
Then,we can obtain:$$getSum(i) = A(1)+…+A(x)\
=A(1)+…+A(i-lowbit(i))+A(i-lowbit(i)+1)+…+A(i)\
=getSum(i-lowbit(i))+B(i)$$We can then easily write the getSum function as follows:
1
2
3
4
5
6
7
8public int getSum(int x){
int res = 0;
for(int i = x; i > 0; i -= lowbit(i)) {
res += bit[i];
}
return res;
}Use the recursive form.
1
2
3
4
5
6public int getSum(int x){
if(x<=0){
return 0;
}
return bit[x]+(long)getSum(x-lowbit(x));
}The complexity of the process is O(LogN) (omitting the process)
Further, if we require
sum(i,j), then we just needgetSum(j)-getSum(i-1).Update
Suppose we have a function
update(i,value)that implements the number at position i plusvalue. Now think about how to implement:Again, take an example:
If we want to
update(6,7), that is, +7 at position 6, then we need to updateB(6) and B(8), according to the diagram above, because the summation terms ofB(6)andB(8)both contain A(6).B(6) = A(5) + A(6);B(8) = A(1)+A(2)+A(3)+A(4)+A(5)+A(6)+A(7)+A(8);So the problem now switches to how to know all the items in the BIT that contain A(i).

Let’s say we we want to find all the BITs that cover A(5).
Firstly: B(5) must be covered.
Second, we need to find the BIT that covers it closest to B(5), i.e. B(6)
Next, we just need to find the BIT that covers B(6) closest to him, i.e. B(8) and so on.
That is, we only need to find the nearest BIT(j) that covers it for the current BIT(i) and update his value.
We can find that:
If BIT(j) is needed to cover BIT(i), then
lowbit(j)>lowbit(i), otherwise it must not be covered, so it can be converted tolowbit(i+a)>lowbit(i)for the smallest a.Because lowbit(i) is the integer divisor of the greatest power of 2 of i, which is also the rightmost 1 of i.
So if
lowbit(a)<lowbit(i), thenlowbit(i+a)<lowbit(i).For example, if
lowbit(j)is 0100 andlowbit(i)is 0010, iflowbit(a+i) must be less than lowbit(i)(because the rightmost 1 must be preserved so a+i will only take the smaller of the right-hand 1 of a and i).When
lowbit(a)=lowbit(i), then the rightmost 1 will be rounded, so the rightmost 1must be shifted to the right, solowbit(a+i)>lowbit(i), must hold, so we can getlowbit(a)=lowbit(i)This allows us to start writing the update function as follows:
1
2
3
4
5
6public void updata(int x,int value){
for(int i = x; i < bit.length; i += lowbit(i)){
//update
bit[i] += value;
}
}
Applications in LeetCode
LeetCode-493
Qa:
Given an integer array
nums, return the number of reverse pairs in the array.A reverse pair is a pair
(i, j)where:0 <= i < j < nums.lengthandnums[i] > 2 * nums[j].
Input:
1
2
3
4
5Input: nums = [1,3,2,3,1]
Output: 2
Explanation: The reverse pairs are:
(1, 4) --> nums[1] = 3, nums[4] = 1, 3 > 2 * 1
(3, 4) --> nums[3] = 3, nums[4] = 1, 3 > 2 * 1Solution
The problem of the stem can be converted into finding how many elements to the left of element j that are 2 times larger than him and summing them.
- Sort the array and discrete map it into an ordered sequence from 1 to n (most questions require this step because the index of a tree array must start at 1, so a mapping of the input parameters is required).
- count the number of occurrences of each number.
- Find the sum of the prefixes of the number of mapped elements to get the number of elements after the mapping, and thus the number of elements before
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61class Solution {
class TrieArr{
long [] arr;
public TrieArr(int n){
arr = new long [n];
}
public int lowbit(int x){
return x&(-x);
}
public int getSum(int x){
if(x<=0){
return 0;
}
return arr[x]+()getSum(x-lowbit(x));
}
public void updata(int x,int c){
for(int i = x; i < arr.length; i += lowbit(i)) arr[i] += c;
}
}
public int reversePairs(int[] nums) {
//nums[i] 和树桩数组的index映射map
//nums[i] and BIT's index mapping map
Map<Long,Integer> map = new HashMap<>();
//对nums元素排序存储,因为要求的是大2倍的数,所以需要把nums[i]*2也加入计算
//Sort and store the elements of nums, because the number required is 2 times larger, so you need to add nums[i]*2 to the calculation as well
TreeSet<Long> set = new TreeSet<>();
for(int i:nums){
set.add((long)i);
set.add((long)i*2);
}
//离散化,并映射
//Discretization, and mapping
int index = 1;
while(!set.isEmpty()){
map.put(set.pollFirst(),index++);
}
//init bit tree
TrieArr bit = new TrieArr(map.size()+1);
//result
int ans = 0;
for(int i = 0; i < nums.length; i++){
//因为是求大于nums[i]*2的出现总次数,那么将所有数字的出现次数-小于等于nums[i]*2出现的次数即可。
//Since we are looking for the total number of occurrences greater than nums[i]*2, it is sufficient to take the number of occurrences of all numbers - the number of occurrences less than or equal to nums[i]*2.
//get the nums[i]*2
long target = (long)nums[i] * 2;
//get bit index
int l = map.get(target);
//total sum - getsum(target)
ans += bit.getSum(map.size()) - bit.getSum(l);
//get nums[i]’s index and update nums[i] occurrences
bit.updata(map.get((long)nums[i]), 1);
}
return ans;
}
}
- #### Similar problems can be found in LeetCode-307 .etc